- the subsequent python dependencies
NOTE: I use the spherical harmonic convention of storing the negative m solutions in the imaginary part of the positive solution. Therfore my index runs from 0 < m < l.
---
The Question:
A tilted dipole can be constructed from its spherical harmonic components, as each component represents a dipole aligned with the x, y, or z-axis.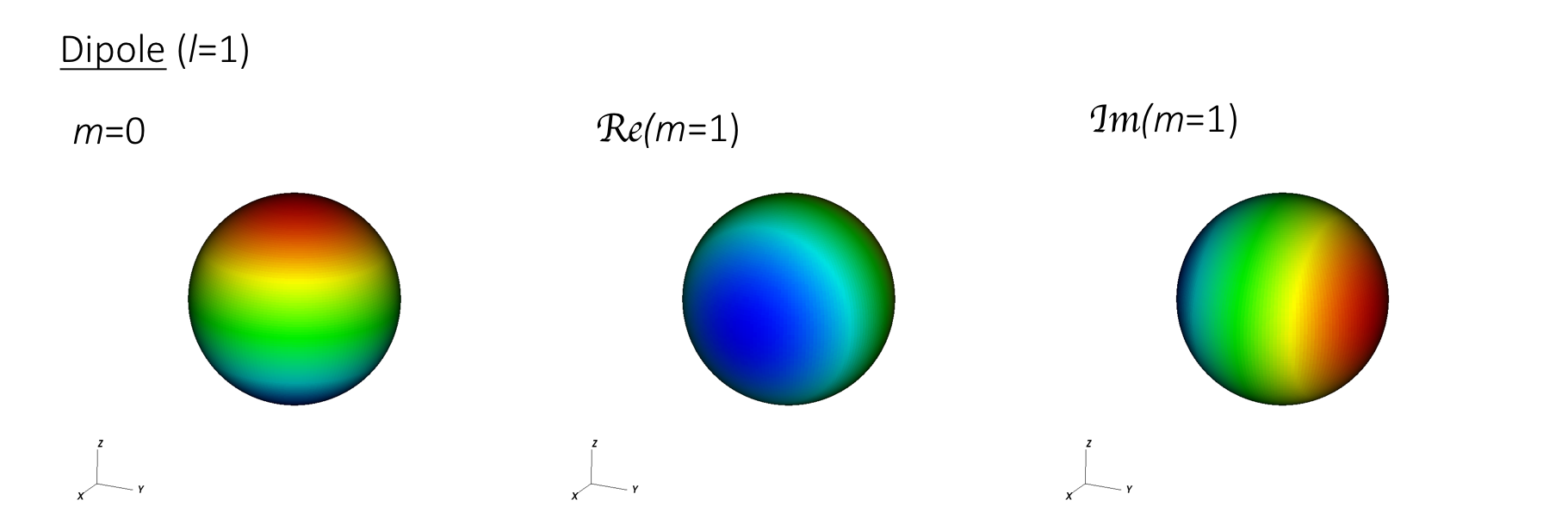
It is not as obvious how tilted geometries can be constructed for the higher order spherical harmonic modes. The various m's produce starkly different arrangements on the surface, unlike the dipole. Here we take interest in the next simplest modes, the quadrupole and octupole:
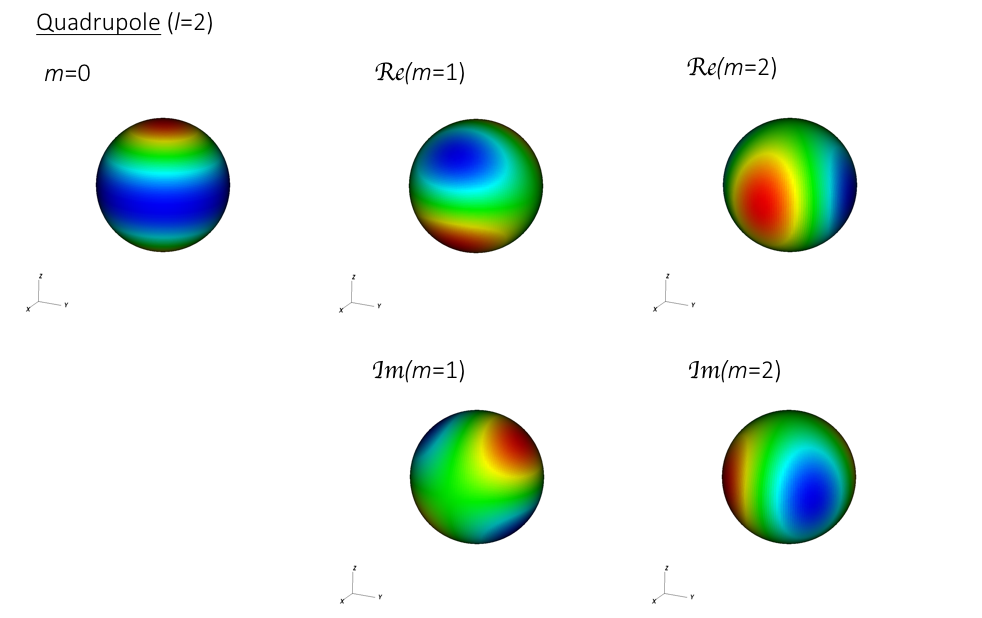
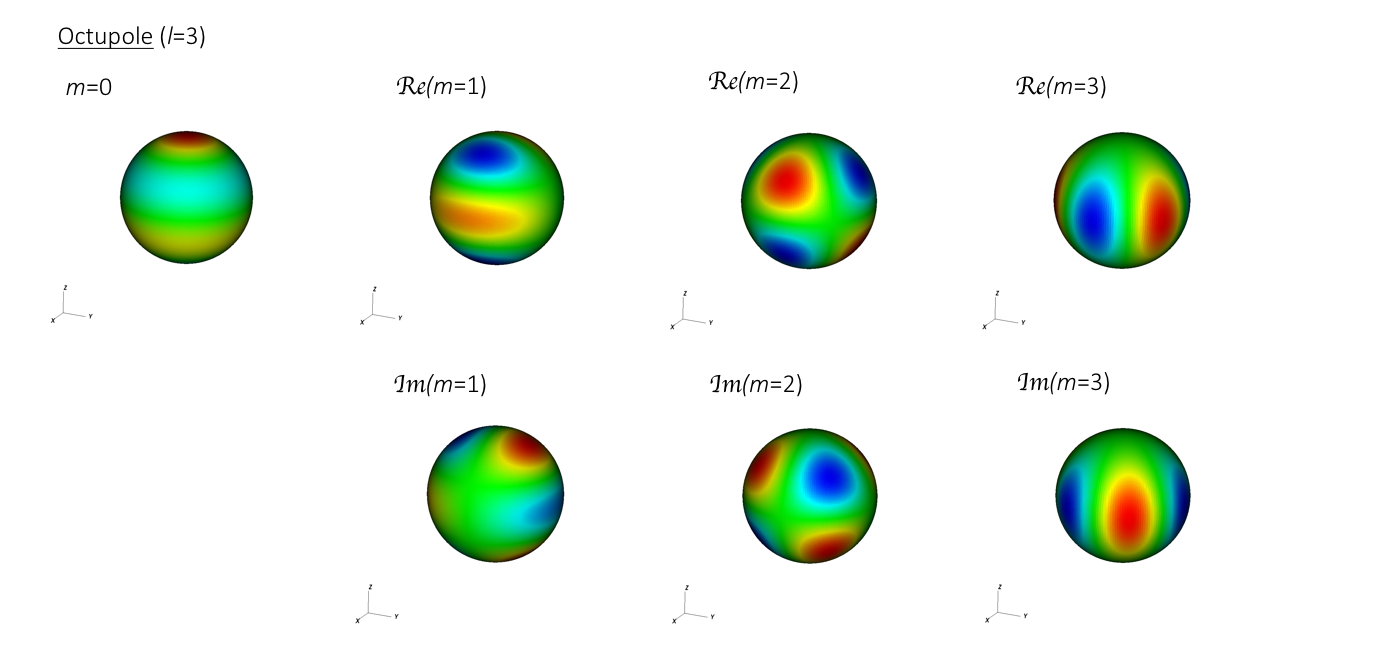
---
Method
To find the combinations of harmonics that comprise the tilted higher order geometries, we artificially tilt a given axisymmetric (m=0) geometry. Then recover the spherical harmonic components using pySHTOOLS. Code available on request.---
Results
The code rotates the coordinate system of the grid, shown in the right-most panel of each figure below. The effect this has on the spherical harmonic decomposition is examined in the middle panel, where the power in each harmonic is measured. During the whole run, the code revolves the geometry by 180 degrees, the values of the coefficients required to construct the tilted geometry are plotted in the left panel i.e. for a given l, Tilted(m=0) = coeff * (m=0) + coeff * Re(m=1) + coeff * Im(m=1) +...etc.Dipole
As the axisymmetric mode (m=0) loses strength, the equatorial (m=1) gains strength. A simple result, which seems obvious.
Quadrupole
The axisymmetric mode (m=0) and the m=2 mode rise and fall together, with the m=1 mode out of phase.
Octupole
A much more complicated behaviour is shown here. The m=1 and m=3 modes have symmetric functions whereas the m=0 and m=2 have antisymmetric functions about the equator.
The code correctly maintains all the power in the given spherical harmonic order. There is a small numerical effect which introduces noise into the other modes, but it is not significant enough to impact our result.
---
Review
This took a good day to figure out, and I think there's some redundant code in there (e.g. there isn't a reason to do the interpolation section as the TH,PHI grid is already equally sampled.) However, this project taught me a lot about the spherical harmonics and coordnate geometry (I hope I don't have to do it the later again for some time). The results show, the power to ofcourse remain within the original mode, and the higher order geometries have a much more complex behaviour that the dipole's.The tilting is done in the z-direction, hence why only the real or imaginary part of each m comes into play. I'de expect to see the opposite result when tilting in the y-direction, maybe with a sign change or two..